Позиционное инвестирование и механизмы динамичного общества

In the coming years and decades, all countries and groups of countries will be under objective and peer pressure to implement major reforms that will enable:

– Fully exploit the potential of human beings as a source of innovative power in society.

– To focus education on specifically human, i.e. non-substitutable artificial intelligence capabilities in conditions where the existing type of artificial intelligence will replace inferior human capabilities (from this point of view, the question of which capabilities make a person human and how the education system should respond to the appreciation of their importance will arise with all urgency).

– Use the growth of leisure time to fully develop specifically human capacities.

– Strengthen the role of productive services, i.e. services aimed at developing, preserving and applying human capabilities (education, health care, education in the family and in the form of culture, social work, etc.), and shift the focus of new quality economic growth to this sector, which will play an increasing role and gradually become dominant.

– Focus the social work sector on overcoming the phenomenon of disadvantage and exclusion, not only of individuals but also of population groups, which is reaching a critical level and requires a gradual reintegration into society.

– Extend the period of voluntary productive employment according to individual possibilities within the framework of a motivating pension system with support for lifelong education, targeted health care, including preventive health care, health resorts and an appropriate corporate culture.

These are challenges that require major economic reforms and are associated with a transformation of the economic basis of society comparable to the Industrial Revolution, but even more significant. As such, they also have significant social, political and geopolitical implications.

In distinguishing prospective reforms in the pension system from pseudo-reforms that orient development towards a dead end, we have used the method of positional investment analysis

We start from our original financial market model conceived as supply and demand of investment funds and investment opportunities, which we complete in the form of a two-component model, allowing us to present this model also as a bargaining game. In doing so, we use the analogy with a similar two-component model presented, for example, by Binmore

We follow this up by refining the tools of theoretical analysis of positional investing so that they can be used to address issues of uniqueness and external authority, which are important and arguably the most important problems in mechanism theory. We show how to unify the tools of positional investing starting from the assumption of neutrality of positional investing and from the requirement to respect the composite nature of payoffs, in which players compare their payoffs in terms of the impact of these payoffs on the future position of the players relative to each other. This is an initial and important result of the refinement of the methods used over the past year. We critically evaluate the contribution of the theoretical tools of positional investment analysis to this issue and, in the discussion of the results, point the way for further research. We formulate a more concrete idea of what might underlie an evolutionarily stable strategy for human societies at the local and global levels under conditions of dynamic technological development.

Figure 1 - A Two-Component Model of the Consumer Goods Market by K. Binmore

Note: source [2. P. 91]

DOI:10.60797/ECNMS.2025.8.2.1

– The sides of the rectangle on the left-hand side of the figure correspond to the quantity of goods.

– The points at opposite ends of the rectangle (bottom left and top right) are the inverted origins of the coordinates corresponding to the quantities of goods obtained by one and the other consumer, in game terminology the player, payoffs are denoted as xA, xB in the total quantities.

– Each point inside the rectangle corresponds uniquely to the distribution of goods among the players.

– The rectangle plots the indifference curves of one player and the other, i.e., the points at which each player benefits equally from different combinations of the two goods.

– The graph shows that only at the points of contact of the indifference curves is the requirement of collective rationality satisfied.

– At the intersection of the indifference curves is the starting point of bargaining (the point of disagreement, or starting point, labeled as "e" on the left and "ξ" on the right in the Binmore figure).

– In the right part of the figure, the same is shown as the Nash bargaining problem.

– The curves, which are terminated by arrows on both sides, express the relation between the left and right parts of the figure.

– Point B is one of the possible solutions to the Nash bargaining problem.

It is in the context of presenting this figure that Binmore points out, "As explained in Section 1.2.3, individual rationality is the requirement that no player receive less than his level of security"

The above relationship is the axis of the development of Hurwicke's views, and a substantial part of his conclusions are situated in the area of its concretization. For example, from a recently published collection of his life's work, one may note: "Consider, for example, an economy consisting of two traders, as conventionally represented by the Edgeworth box, with classical strictly convex indifference curves and positive suboptimal initial endowments of both goods for both traders. We have already noted that if both of them were told to behave as price takers, it would pay one of them to break this rule if he could get away with it. We now assume that he cannot openly violate the rule, but can "pretend" to have preferences other than his actual preferences. The question is whether he could invent a fake (but convex and monotonic) preference map that would be more advantageous to him than his true one, assuming that he follows the rules of accepting prices according to the fake map, while the other trader plays the game honestly. The answer will easily turn out to be yes. Thus, in such a situation, the rules of perfect competition are not incentive compatible"

Here is our two-component model of the financial market where the supply and demand of investment funds and investment opportunities meet, which has some specificities compared to the above. This model can be used to formulate a number of conclusions that build on the research carried out in the Hurwicz framework, i.e. in the design and implementation of mechanisms that allow to solve some of the problems raised by the evolution of society.

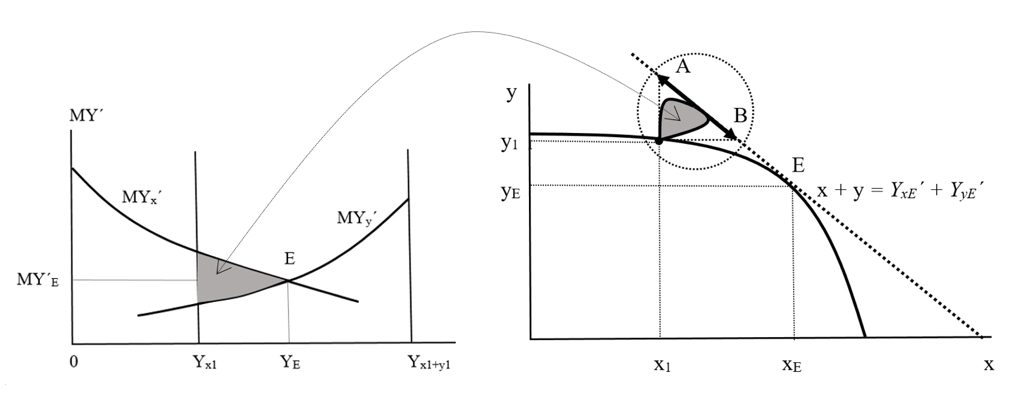
Figure 2 - The two-component model of the financial market (our original model)

Note: own creation [3].

Yx, Yy is the simultaneous income of one and the other player;

Yx1, Yy1, the specific amount of investment funds (current income) available to the players;

Yx´= x, Yy´= y is the future income of one and the other player (which are also the returns on the investment opportunities available to the players);

MYx´ = MYx´(Y), MYy´ = MYy´(Y) are the marginal return functions of the investment opportunities available to the players, and simultaneously the supply and demand curves of investment funds and investment opportunities

DOI:10.60797/ECNMS.2025.8.2.2

– The left side of the figure is a microeconomic model of the financial market in the marginal variables in terms of supply and demand of investment opportunities and investment funds (consisting of current income), the grey area highlights the area of Pareto improvements due to the fact that investment funds of one player are used to realize more profitable investment opportunities of the other player.

– The right-hand side is the same expressed in total quantities (x, y). The dotted line shows the set of points of the maximum sum of payoffs, the area of Pareto improvements is also highlighted by the grey area.

– The bolded line with arrows at the ends shows the set of all points that satisfy the requirements of attainability, individual rationality and collective rationality.

(MYx´(Y))´ < 0, (MYy´(Y))´< 0, are the first derivatives of the marginal return function of the investment opportunities available to the players. These functions are non-increasing, i.e., players exploit investment opportunities according to their rate of return, which can also be seen as a condition on the individual rationality of players. By integrating these functions, the relationship between the two components of the graph can be expressed analytically.

The two two-component figures show that there are a large number of points in the distribution of payoffs among players that satisfy the requirements of attainability, individual and collective rationality (the problem of ambiguity of solutions without additional conditions arises). There is a significant difference in the commodities that enter the market. In the one case, these are goods, in the other case, investment funds and investment opportunities (especially in the case of investment opportunities, they are significantly different commodities). In the Binmore model, the non-comparability of payoffs (returns) is crucial, whereas in the financial market model, not only are the returns comparable, but each player can transfer part of his returns to the other player. This is one of the reasons why it makes sense to consider the maximum amount of payoffs when looking for a solution. The maximum payoff amount is outside the original set of possible revenue distributions.

In his pioneering work, Nash

– They can compare the distribution of payoffs among themselves (and, for example, a 90:10 distribution, as empirical experiments from ultimatum games show) may become so unfair to one of the players as to be unacceptable to him

– A larger role is also played by reasoning in terms of time. When exchanging consumption goods, a player considers only his expected utility; when making decisions in the financial market, he considers a longer time horizon and hence the consequences for him of the other player's larger or smaller payoff.

Although the two models are quite different at first sight, there are intermediate or mixed states, one model transitioning quite smoothly into the other. We show what is the main reason for the difference between the two models:

– Consumption of a consumption good generates a utility to the consumer that is incommensurable with the utility of the other consumer and is non-transferable. In order to obtain the consumption good, we have to spend some resources; in the case of using Edgeword's box plot, we have to sacrifice some amount of the good we own to obtain some amount of the good we want to obtain.

– By using present income as an investment means (what we invest) to realize a certain investment opportunity (what we invest), we obtain a certain future income that is comparable in the same units to the income of the other subject (the one who uses his investment opportunity) and can be shared with the other subject, or if he provides his investment means to realize the investment opportunity of the first subject, he must share this income with him.

The consumption of a consumption good (as the use of a consumption opportunity) may at the same time be more or less directly a source of income, i.e. the use of a consumption opportunity may take the form of the use of an investment opportunity. As early as the 1920s, Pigue

Undoubtedly, in many cases, consumption of a consumption good (as the use of a certain consumption opportunity) can at the same time be more or less directly a source of income, i.e. it can take the form of the use of a certain consumption opportunity in the form of the use of an investment opportunity. We may not be aware of this, but we behave accordingly.

If the effect of the use of investment opportunities (consumption opportunities in the form of productive consumption) is to be manifested, coupled with a financially valued and financially transferable return, mechanisms allowing credit financing may operate. It does not always have to be finance. One can imagine a relationship between two landowners, one of whom has sufficient water and the other scarce, in the sense that, using its own water supply, the yield from the last unit of land irrigated by one landowner is greater than that of the other landowner. Both can increase their yield in a similar manner as if they were in a lender and borrower relationship, if the one who has provided his water receives from the other a portion of the yield thus increased. Similar examples involving other commodities may also be imagined in any number of ways, and are commonly found in real life.

There are two areas in which there may be a more or less smooth transition from one binary graph to another:

– The conversion of non-transferable utility from consumption goods into transferable financial resources.

– The credit superstructure in the exchange of goods, which can take various forms.

The comparability of returns and the possibility of using them in the future raises the questions: is any distribution of returns between two players acceptable to both? Is each player indifferent to the other player's payoff? These and similar considerations (albeit mostly unconscious) also manifest themselves in decision making in ultimatum games. From this point of view, rejecting a 90:10 split with the expectation that the rejecter will lose 10 units is not a failure of rationality, but a manifestation of a higher rationality (the player is not making a short-sighted decision).

The projection of the idea of future developments into the present decision can also occur in the case of a normal exchange of consumption goods. But usually we do not care too much about what the other's utility will be; we may even enjoy the other's utility in the form of pleasure. If, however, the result is funds that can be used by the other player to strengthen his position in deciding how to share, we must begin to take seriously the condition of acceptability of the distribution of payoffs. That one player can use their payoff to influence the distribution of payoffs in their favour in the next round is what we call positional investing. This is a phenomenon whose theoretical analysis we will use to answer some of the substantive questions related to the reforms discussed in the introduction to this paper.

The fact that very often, and sometimes in a substantial way, a player projects an idea of future developments into current income distribution decisions (in the more general case, into decisions about his choice of strategy when he can or must participate in a particular joint action) is undeniable, unmissable and significant. There are two ways to express this in standard joint action revenue sharing problems:

a) A path based on the assumption that there is a set of mutually acceptable distributions that is a subset of the set S, and the solution must belong to this set.

b) A path based on the assumption of the existence of two payout components, i.e. a composite payout consisting of two components.

These are different starting points, different ways of looking at the issue, different ways of grasping it.

Ad a) A path based on the assumption of the existence of a set of mutually acceptable distributions:

Suppose that a situation has arisen where not every distribution that satisfies the conditions of individual rationality, collective rationality and reachability is, for certain reasons (for which it will be necessary to give a strong interpretation), acceptable to both players, i.e.: Sa ⸦ S, where Sa is the set of mutually acceptable distributions. In the intentions of the above, one can distinguish: SaX the set of acceptable distributions for player X, SaY the set of acceptable distributions for player Y. SaX ∩ SaY ≡ Sa, i.e., the set of mutually acceptable distributions is the intersection of the sets of acceptable distributions of each player The solution of the corresponding problem, i.e., the payoff distribution, then, in addition to the aforementioned assumptions of individual rationality, collective rationality, and reachability, must satisfy the acceptability condition, which can be simply formulated as follows: (x, y) 󠇪∈ Sa. If the set Sa takes the form of a relationship between the payoffs of two players such that the increment in the payoff of one player (Δx) must be compensated by a uniquely given increment in the payoff of the other player (Δy), we can speak of a function of acceptable solutions (y=a(x)) and its progression. In the simplified case (which is suitable for graphical representation and verbal description of various situations) we can speak of the line of acceptable solutions and its slope: y = xa + a.x, where the constant xa determines the position of the line, the coefficient and its slope.

Ad b) A path based on the assumption of a composite final payoff:

The composite final payoff path, which takes into account the fact that what one or the other player gets from the distribution of the payoffs also affects the valuation of the payoff by the other player. In terms of expected evolution, one can assume a situation where one or both players assess the outcome of the payoff distribution from the joint action not only in terms of what each player gains for himself, but also in terms of what the other player's payoff will mean for himself (i.e. for the first player). One way of expressing this is to distinguish between two components of the players' payoffs: the primary payoff (what each player receives as the agreed outcome of the distribution of the proceeds of the joint action); the adjustment (how much a player is willing to reduce his payoff or, conversely, demand an increase in his payoff in terms of the consequences of the primary payoff distribution).

One possible expression of the payoff adjustment is the following equation:

x = xp + aX(x, y)

y = yp + aY(x, y),

where xp, yp are the primary payoffs, aX(x, y), aY(x, y) are payoff adjustments based on the anticipation of future developments by either player.

If we perform a linear approximation, we obtain the following equation:

x = xp + a(x - y) from which the payoff of the other player can be derived.

The two paths connect. We will consider only the simplified case of the linear approximation. From the above it follows:

(y = xa + a.x)˄(y = xp/ap + (1-1/ap).x)

And it follows for the value of the constant and the coefficient of the linear equation:

(xa = xp/ap)˄(a= (1-1/ap))

This is a non-trivial result. Two different paths led us to the same result. The fact that we only considered a linear approximation is irrelevant. This can also be expressed graphically. Recall the case of dividing a certain amount (the ultimatum game), where one proposes a division, the other either agrees or disagrees, in case of agreement the amount is shared, in case of disagreement no one gets anything. In a sense, this game is involved in the players' decision-making in EVERY joint action, which results in a surplus over cost that they can divide between themselves. It is even contained in every conflict resolution option, because that resolution also produces a surplus over costs that the players can divide among themselves.

In the set of payoffs that represent an improvement over the initial state, if collective action and subsequent payoff sharing occurs, we distinguish between those elements of the set that are acceptable to both players and those that are unacceptable to either or both players. We call this payoff set the positional investment neutrality set, i.e. the set whose elements are distributions that do not allow either player to improve his position relative to the initial state. In this case, the composite payoff of each player is simultaneously non-negative.

If this set takes the form of a relationship between the payoffs of two players such that the payoff gain of one player must be compensated by a uniquely given payoff gain of the other player, we can speak of a position neutrality function (y=N(x)) and its progression, see the following figure.

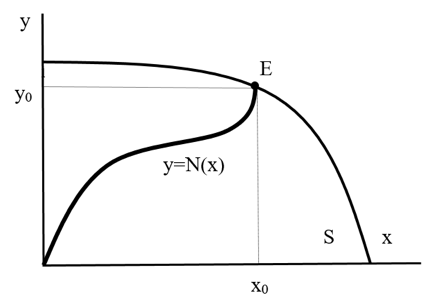
Figure 3 - Position neutrality function

Note: own creation.

x, y players' payoffs;

S the set of available payoffs;

y=N(x) position neutrality function;

E the equilibrium point, or the point that satisfies the condition of individual rationality, collective rationality, reachability and neutrality of positional investing

DOI:10.60797/ECNMS.2025.8.2.3

In the simplified case (which is suitable for graphical expression and verbal description of various situations) we can speak of the neutrality line of positional investment and its slope.

The explanation coming from the neutrality of positional investing is based on the fact that the subjective valuation of the payout by individual players includes the consideration of the possibility of using the payout to strengthen their position:

Figure 4 - Positional neutrality line

Note: own creation

DOI:10.60797/ECNMS.2025.8.2.4

The function or line of positional investing neutrality is a similarly "powerful" tool for analyzing positional investing as indifference curves are in expressing consumer preferences. It makes visible what has been hidden and enriches thinking in the field by adding an important dimension.

It would seem that, through the positional neutrality condition, we solve the problem of both uniqueness and external authority: add the positional neutrality condition, and we have a solution that is unambiguous and that does not need to rely on external authority. Each player must respect how the other player sees and values the situation if joint action is to occur.

We consider the case where a player can turn a property or income advantage into an instrument of discrimination against the other player, and the other player is aware of this. As long as the player is not making a myopic decision (valuing his payoff not just in terms of immediate utility), he is also reflecting expected future developments in his decision. Non-short-sighted decision-making is characterized by a higher degree of rationality than short-sighted decision-making; if theory is to serve a higher degree of rationality in player decision-making, it should not be satisfied with models of short-sighted decision-making alone. This corresponds to the situation where a player decides not only on the size of his payoff but also on the size of the other player's payoff. The inclusion of an analysis of the phenomenon of positional investing makes it possible to clarify an apparent paradox in the ultimate game, e.g., why a player rejects a proposal to split a certain amount of money 10:90 to his disadvantage, even though he loses the amount of 10 (for a summary, see

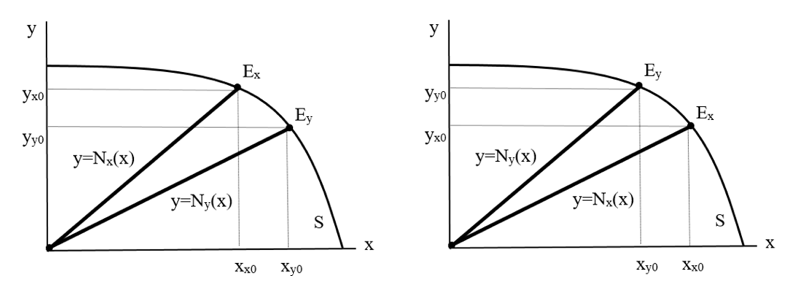
Figure 5 - Different players' views of the neutrality line

Note: own creation.

x, y players' payoffs;

S set of available payoffs;

y=Nx(x) the neutrality function of positional investing as seen by player X;

y=Ny(x) neutrality function of positional investing as seen by player Y;

Ex the equilibrium point, i.e. the point that satisfies the condition of individual rationality, collective rationality, reachability and neutrality of positional investing as seen by player X;

Ey point of equilibrium, i.e. the point that satisfies the condition of individual rationality, collective rationality, achievability and neutrality of positional investment as seen by player Y;

xx0, yx0 player payoffs at the equilibrium point as seen by player X;

xy0, yy0 player payoffs at the equilibrium point as seen by player Y

DOI:10.60797/ECNMS.2025.8.2.5

– In the case on the left, each player demands less for himself than the other player is willing to offer; there is room for agreement.

– In the case on the right, each player demands more for himself than the other player is willing to offer; there is no room for agreement.

The reason for the different vision is not a lower level of rationality, but a different awareness of future developments, which must be taken into account even in very general models. If the disagreement is due to a different appreciation of what distribution of payoffs is acceptable to each player and what is not, and if that different appreciation has its origin in a different vision of future developments, then negotiation may achieve greater consensus on the view of future developments, but it does not fully or sufficiently address the problem of clarity and the need for external authority. Nevertheless, the inclusion of this condition widens the scope for applying rational elements of the approach to solving socially significant problems. If the disagreement arises from a different appreciation of what distribution of payoffs is acceptable to each player and what is not, and if that different appreciation is rooted in a different vision of future development, then a greater consensus on the view of future development can be achieved through negotiation, and possibly the use of an external authority to play a more methodological role in fleshing out and possibly converging ideas about future development.

The methodological implications tell us that the more the participants in a joint action converge on a common view of the future, i.e. specifically 'what happens when', the closer they come to agreement. Whether this convergence of views on the future is the result of their own activity or under the influence of a commonly recognized external authority. There is a complement to this conclusion – if someone wants to divide the participants in a joint action (as an external "friendly" authority), they will present them with a false picture of future developments, which will give each or one of the players a distorted picture of "what happens when". Reality shows that this "divisive" approach can be very effective.

Mechanism theory (its design, enforcement and institutional support) will grow in importance in promoting comprehensive reforms. Within this, the role of tools for analysing the phenomenon of positional investment in addressing the issue of the clarity and enforceability of proposed solutions will also grow.

Positional investing is associated with the operation of mechanisms that increase the return on investment opportunities of one player at the expense of reducing the return on investment opportunities of the other player, while at the same time reducing the efficiency of the economic system. Therefore, it is necessary to search for such mechanisms that will promote the use of investment opportunities, their implementation brings not only an increase in income to a certain player, but increases the profitability of investment opportunities of other players. These are investment opportunities that are, in a sense, the opposite of positional investing and significantly increase the efficiency of the whole system. In a forward-looking way, one can consider, for example, linking the creation of university alumni networks with creative teams based on the principle of complementarity.

The fact that universities, and the effects of their activities in the educational and scientific spheres, will have to play a significant role in solving the current problems is probably obvious to anyone with a realistic view of current events. One of the outcomes of the paper is the specification of the way in which they can respond to current events in accordance with the objective requirements given by the development trends and the form of the accumulated problems. It is to be expected that research in the area of specifying a prospective solution based on identifying investment opportunities with positive synergies for other players (which is in a sense the opposite of positional investing) and promoting them through appropriate mechanisms will yield as fruitful results as identifying the problems that arise as a result of the phenomenon we have called positional investing.